Una vez contextualizado, en otros artículos, el concepto de razón a lo largo de la Historia, los autores Oller y Gairín (2013), mencionan que, en los libros de texto recientes sobre la enseñanza de la proporción, no existen evidencias de la razón entre cantidades de una misma magnitud, así como tampoco definiciones de la razón entre cuantías de magnitudes diferentes. Para ambos autores, esto tiene como consecuencia que los problemas de las magnitudes acaban convirtiéndose en resolver problemas de forma mecánica y no razonando matemáticamente, usando algoritmos como la Regla de Tres.
Los autores dan como posible solución a las situaciones en las que la proporcionalidad trae consigo una relación entre dos magnitudes como mínimo, el añadir la idea de razón entre cuantías de distintas magnitudes, ya que puede aclarar cómo el alumno percibe la situación. En síntesis, se trataría de reforzar la visión de los matemáticos chinos frente a los griegos.
En relación a este apunte que realizan los autores, durante las prácticas de docente, para que los alumnos fuesen conscientes de este problema, se les entregó una relación de ejercicios en las que no siempre existía relación de proporcionalidad multiplicativa. Sin embargo, debido a su mecanización, los alumnos resolvieron todos los ejercicios mediante Regla de Tres, realizándolos de forma incorrecta.
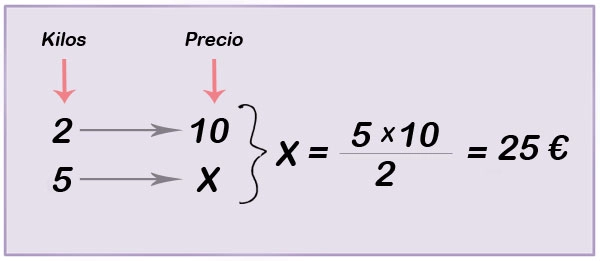
Ejemplo del choque entre el paradigma griego y el chino, podemos encontrarlo en muchos de los ejercicios tipo de cualquier libro de texto. Los autores, eligen el siguiente: “Una fuente arroja 42 litros de agua en 6 minutos, ¿cuántos litros arrojará en 15 minutos?” (Oller y Gairín, 2013, p. 335).
Desde la perspectiva griega, distintas magnitudes no pueden relacionarse entre sí. Por lo que, construyen la razón utilizando las magnitudes de tiempo y buscan una equivalente para las magnitudes de la cantidad de agua que arroja la fuente.
Sin embargo, desde la perspectiva china, distintas magnitudes si pueden relacionarse, de donde fijarían la razón dada en el enunciado, considerando el par (6, 42), que nos relaciona la magnitud de tiempo con la de la cantidad de agua que la fuente arroja. De esta manera, deben encontrar un número cuya razón sea equivalente al primer par, con la restricción de que el elemento que ya conocemos es 15.
Como dicen Oller y Gairín (2013), y puede observarse, desde una óptica estrictamente numérica, ambas disposiciones son equivalentes, independientemente de si usamos el enfoque griego o chino. En cuanto a sentido son distintos e irreconciliables, dependiendo del punto de vista de quien resuelva. En el primer enfoque, se realiza el cálculo de la razón entre mismas magnitudes, por lo que un matemático chino dispuesto a resolverlo, se cuestionaría el por qué no se relacionan las magnitudes de tiempo y litros de forma conjunta. Mientras que el segundo enfoque carecería de sentido para un griego, ya que la concepción griega no permite mezclar las magnitudes de litros con las de tiempo.
En la actualidad, el conflicto de ambas visiones sigue vigente, por lo que sería muy productivo para el alumnado el estudio de ambas, con el fin de conseguir una mejor y amplia comprensión de dicho concepto. Sin embargo, para Oller y Gairín (2013), el enfoque chino proporciona operaciones con mayor sentido, y, por tanto, mejor comprensión de la tesitura.
Estas diferencias entre posturas, así como las distintas maneras de observar, analizar y resolver el mismo problema, pone de manifiesto la necesidad de otorgar a los alumnos la capacidad de discernir y razonar matemáticamente. Para ello, se les debe armar con las herramientas necesarias para que puedan relacionar razones, acercándose a la perspectiva griega, o bien relacionando magnitudes, teniendo una visión asiática. Conocer como el concepto de proporción ha evolucionado a lo largo de la Historia y cómo ha sido su aplicación a través de la misma, dependiendo del paradigma, sirve para entender las fortalezas y debilidades de ambas visiones, lo que resulta de gran valor a la hora de acercar el concepto a los estudiantes y facilitar superar las dificultades que vayan a acaecer durante el proceso de enseñanza-aprendizaje. Durante la Unidad Didáctica, se hará uso, en sus inicios, de ambas concepciones, utilizando levemente la griega para introducir el concepto de razón desde una visión más numérica. No obstante, la perspectiva china resulta más visual al alumnado, tendiendo a relacionarse más fácilmente con el algoritmo de la regla de tres y con sus conocimientos previos, por lo que será el método ganador en la nueva Unidad Didáctica.
¿Te ha parecido interesante este artículo? Si es un sí, ¡me gustaría leer tu opinión en los comentarios! Y si te estás planteando contratar clases particulares online de matemáticas, puedes contactar conmigo y te responderé a la mayor brevedad posible. 🙂




